数据存储与内存 | Data Storage and Memory
一、回顾与引入
在上一节里,我们从数学的角度讨论了进制的概念,以及如何在不同进制之间转换。但如果要把一种数据(例如数字、字符、图像等)存储到计算机中,我们不禁要问:这是怎么实现的呢?和我们所学的二进制又有什么关系?
在这一节中,我们将着重探讨这样一些问题:
内存是什么?内存是怎么工作的?不同类型的数据在内存中是如何存储的?不同类型会占用不同的内存空间么?
回答这些问题,对我们理解常量、变量的工作原理,以及后续学习数组、结构体、指针等内容都有很好的铺垫作用。
和上一节一样,作为基础知识系统化的一环,我们仍然希望你能以理解为主。如果理解了原理,后续的学习和应用会变得轻松许多。
二、什么是内存?
这里有一个广为流传的笑话:
小明觉得自己的电脑硬盘空间不够用了,于是告诉电脑城老板:“能不能帮我换个大点的内存?”老板欣然答应,给小明换了一块更大的内存条。小明回家后发现,电脑的硬盘空间还是没变大。气冲冲地回到电脑城质问老板:“你不是说换个大点的内存吗?为什么我的硬盘空间没变?”老板无奈地解释道:“内存和硬盘是两回事啊!”
内存(Memory)和硬盘(Hard Disk)是计算机中两种不同的存储设备。简单来说:
- 硬盘:长期存储数据的地方,关机后数据依然存在。例如我们常说的
C盘、D盘等,都是硬盘的一部分。你的文档、图片、程序文件等都存储在硬盘上。 - 内存:计算机程序运行时临时存放“数据”的地方。内存的读写速度远快于硬盘,因此是CPU处理数据的主要场所。
当我们打开一个程序时,操作系统会把程序从硬盘加载到内存中,CPU再从内存中快速读取数据进行处理。关机后,内存中的数据会全部丢失。
数据的“大小”单位:位与字节
在计算机中,数据通常是以二进制的形式存储的。例如内存中可以记录一串二进制数据:10110011。在内存中,有若干个(很多很多)“空位”来存放一个二进制数码。也就是说,这样一个空位的值要么是1,要么是0。
每个这样的“空位”称为位(bit)。例如这里的例子10110011,它使用了内存中的8个位来存储。
单个的位只能表示两种状态(0或1)。这实在是有点太少了。但如果我们把8个位组合在一起,通过0和1的组合就可以表示更多的状态。像这样8个位组成的单位称为字节(Byte),即:
1 \text{ Byte} = 8 \text{ bits} 因此,一个字节可以表示2^8 = 256种不同的状态(从00000000到11111111)。如果从二进制向十进制直接转换,我们知道这样一个字节可以表示0到255之间的整数。
同样,字母A到Z只有26个,因此理论上也可以用一个字节的空间来表示。这就涉及到编码(coding)的概念。简单来说,对于非数字类型的数据,例如这里提到的A到Z,我们给每个字符分配一个唯一的数字编号,例如A对应1,B对应2,以此类推。然后用这个编号对应的二进制数来存储这个字符。这样,我们就可以用二进制来表示更多类型的数据了。
关于字符、浮点数、字符串等类型具体是通过什么方法存储的,我们会在后续章节中详细介绍。
三、数据类型与内存分配
1. 数据类型是怎么工作的
我们在1.2节中学习变量时就提到过,每一个变量有它指定的数据类型,例如整型int、字符型char、浮点型float等。
事实上,指定一个变量的数据类型并声明它的过程,就是告诉计算机:我要在内存中为这个变量分配一块特定大小的空间,用来存储这个变量的数据。
每一种数据类型都有它对应的内存空间大小。因此,不同数据类型能存储的数据范围也不同。
2. 数据类型对应的内存空间大小
下面是一些常见数据类型及其对应的内存空间大小:
| 数据类型 | 常见占用字节数 |
|---|---|
| char | 1 字节 |
| short | 2 字节 |
| unsigned short | 2 字节 |
| int | 4 字节 |
| unsigned int | 4 字节 |
| long | 4 字节 |
| unsigned long | 4 字节 |
| long long | 8 字节 |
| unsigned long long | 8 字节 |
| float | 4 字节 |
| double | 8 字节 |
| long double | 16 字节 |
是不是有些眼花缭乱?这里出现了一些我们曾经没有遇到的数据类型。我们把这个表格拆成三部分:
- 字符型
char
占用1字节,能表示2^8=256种情况,其中0-127分别对应着常用的128个字符。 - 整数类型
short、int、long、long long,及其无符号unsigned形式
分别占用2、4、4、8字节。分别能表示65536、4294967296、4294967296、18446744073709551616种情况。它们能表示的整数范围不同,我们也将马上介绍它们能表示的整数范围。 - 浮点类型
float、double、long double
分别占用4、8、16字节。它们能表示的小数范围和精度不同,我们将在后续章节中详细介绍。
举个例子:当我们声明一个变量 int age = 18; 时,由于这个变量age是int类型,通过上面的表格我们知道,计算机会自动在内存中为它分配4个字节的空间,像这样:
00000000 00000000 00000000 00000000这4个字节专门用来存储age的数值。当我们同时对它初始化为18时,计算机会把18的二进制表示10010,存入这4个字节中:
00000000 00000000 00000000 000100103. 示例:不同数据类型的内存分配
假设我们有如下代码:
char gender = 'M';
int age = 18;
float height = 1.75;
double weight = 65.5;计算机会分别为这四个变量分配如下空间:
gender占用1字节age占用4字节height占用4字节weight占用8字节
这些空间在内存中是“连续”摆放的吗?并不一定,具体排列方式与编译器相关,但每个变量都拥有自己独立的一块空间。
四、数据的表示与储存
我们现在知道,每一种数据类型的变量,在内存中都有一块特定大小的空间。那么像123、-5、'A'、3.14这样的数据,是如何存储在这些空间中的呢?我们针对上面讲的三类数据类型,分别简单介绍它们的存储方式。
1. 字符型数据的存储:ASCII编码
我们前面提到,字符型数据char占用1字节(8位),能表示256种状态。那么计算机是怎么把每一种状态和具体的字符对应起来的呢?这里我们介绍一种最常用的编码方式:ASCII编码。
ASCII编码(American Standard Code for Information Interchange,美国信息交换标准代码)是一种字符编码标准,它为128个字符分配了唯一的数字编号。包括:
- 大写字母
A-Z:对应编号65-90 - 小写字母
a-z:对应编号97-122 - 数字
0-9:对应编号48-57 - 常用符号(如
+、*、!、@等)和控制字符(如我们在前面学习里提到的换行符'\n'、字符串结束符'\0'等)
这样,对于ASCII编码中的这128个字符,存储在char类型中实际上是存储了它们对应的编号的二进制表示。例如:
- 字符
'A'对应编号65,二进制表示为01000001; - 字符
'a'对应编号97,二进制表示为01100001; - 字符
'0'对应编号48,二进制表示为00110000;
等等。
我们在这里给出完整的ASCII编码表,供参考:
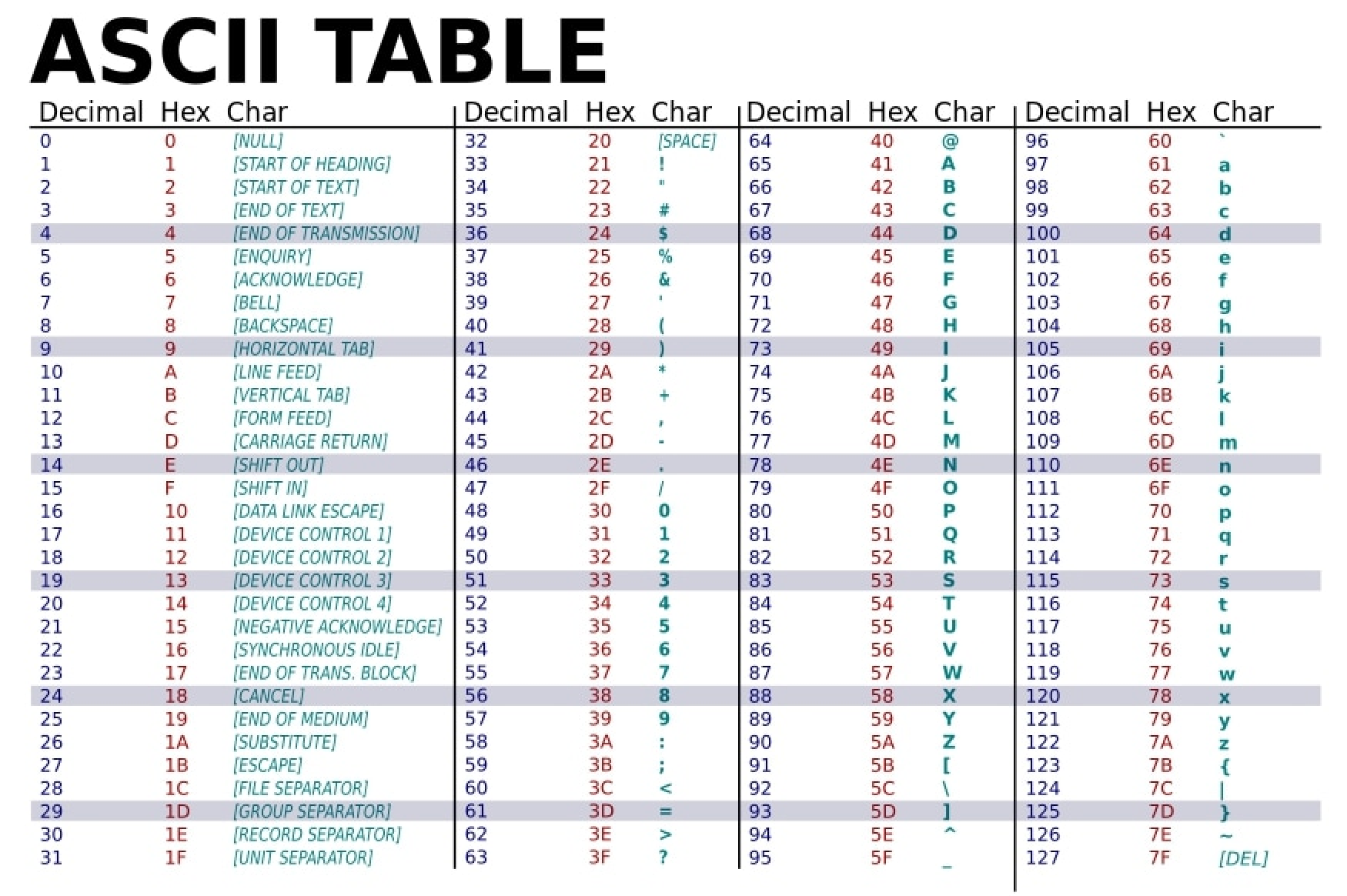
作为扩展:
char类型能表示256种状态,但ASCII编码只定义了128个字符。剩下的128个字符呢?这是由于世界上不同国家和地区的文化使用了不同的字符,剩下的128个状态通常用于扩展字符集,存储该国家或地区的特定字符。
且对于扩展字符集128-255中的字符,在不同国家的计算机系统中对应的字符可能不同。思考:汉字可以被存储在
char类型中么?想想'汉'这样的写法是合法的么?猜一猜是为什么?
2. 整型数据的存储
我们已经对整型int比较熟悉了,而我们上面列出的short、int、long、long long其实也都属于整型数据。他们分别被称为短整型、整型、长整型、长长整型,都可以用于存储整数。
它们的区别在于能表示的整数范围不同,这是因为它们占用的内存空间大小不同,分别是2、4、4、8字节。
那么,整数是怎么存储在内存中的呢?这些整型能表示的范围具体又是怎么计算的、是多少?我们这里以(普通的)整型int为例,来说明整数的存储方式。
无符号整数的存储
在讨论我们常用的int类型之前,我们先来看看无符号整数(unsigned int)的存储方式。
在计算机诞生之初,人们设计变量存储数据时,并没有考虑存储负数的需求,因此最初的整数类型只能表示非负整数(即0和正整数)。这样的数据类型就被称为无符号整数。
无符号整数,顾名思义,就是没有正负号的整数。它只能表示0和正整数。它的表示方式很直接,就是把整数的二进制形式直接存储在内存中。
例如:
unsigned short a = 5;
unsigned int b = 300;
unsigned long long c = 12345678901234;在内存中,a、b和c分别被存储为:
a: 00000000 00000101
b: 00000000 00000000 00000001 00101100
c: 00000000 00000000 00000000 00001011 00111010 01110011 11001110 00101111 11110010因此,对于含有4个字节,32位的无符号整数unsigned int,它能表示的整数范围是:
0 ~ (2^32 - 1) = 0 ~ 4294967295对于short、long、long long,同理可以得到它们能表示的无符号整数范围分别是:
| 数据类型 | 能表示的无符号整数范围 |
|---|---|
| unsigned short | 0 ~ 65535 |
| unsigned int | 0 ~ 4294967295 |
| unsigned long | 0 ~ 4294967295 |
| unsigned long long | 0 ~ 18446744073709551615 |
有符号整数的存储
可在我们之前的学习中,我们已经利用int类型存储过负数了。那么,int类型是怎么存储负数的呢?它和无符号整数有什么区别?
int类型是有符号整数(signed int),它能表示正整数、负整数和零。为了区分正负数,计算机使用int类型32位中的最高位(即最左边的一位)作为符号位,这一位0表示正数,1表示负数,其余31位用于表示数值。
对于正数,由于最最高位是0,因此它的存储方式和无符号整数是一样的。例如:
int x = 5; 在内存中,x被存储为:
x: 00000000 00000000 00000000 00000101对于负数,表示方法有些许的复杂。计算机采用这样的方式:先将该数的绝对值转换为二进制形式,然后对所有位(对int来说,就是全部的32位)取反(即0变1,1变0),最后加1。
例如:
int y = -5; 在内存中,y是这样被储存的:
首先,5的二进制表示是:
00000000 00000000 00000000 00000101然后,对所有位取反,得到:
11111111 11111111 11111111 11111010最后,加1,得到:
11111111 11111111 11111111 11111011这样的表示方法,称为二进制补码(Two's Complement)。诚然它并不直观,甚至有些复杂,但它仍然有不可替代的优点,例如
- 很重要的一个性质是,两个相反数的二进制表示相加,结果为
0 - 拓展地说,计算机可以用同样的电路来处理加法和减法运算。
因此,对于含有4个字节,32位的有符号整数int,由于这32位中的最高位用于表示符号,所以只有剩下的31位来表示数据的绝对值。它能表示的整数范围是:
-(2^31) ~ (2^31 - 1) = -2147483648 ~ 2147483647对于short、long、long long,同理可以得到它们能表示的有符号整数范围分别是:
| 数据类型 | 能表示的有符号整数范围 |
|---|---|
| short | -32768 ~ 32767 |
| int | -2147483648 ~ 2147483647 |
| long | -2147483648 ~ 2147483647 |
| long long | -9223372036854775808 ~ 9223372036854775807 |
3. 浮点型数据的存储(较复杂)
浮点型数据用于表示带小数的数值,例如3.14、-0.001、2.0等。由于浮点数的表示和存储较为复杂,我们这里只做一个简单的介绍。
直观地看,浮点数与整数相较,除了需要保存数值本身外,还需要保存 “小数点在第几位” 的信息。因此,对于浮点数,我们需要设计一种专门的标准来利用好它们的内存空间,存储这些信息。
浮点数的存储通常遵循IEEE 754标准。以float类型为例,它占用4个字节(32位),这32位被划分为三部分:
- 符号位(1位):表示数值的正负,
0表示正数,1表示负数。 - 指数部分(8位):用于表示“小数点的位置”。
- 尾数部分(23位):用于表示有效数值。
我们通过一个例子简要说明这个标准的存储规则:
假设我们要存储浮点数-5.75,它的二进制表示是-101.11。按照IEEE 754标准,我们需要进行以下步骤:
- 符号位:由于
-5.75是负数,最高位(符号位)为1。 - 记录小数点的位置:直观地说,对于
-101.11,小数点出现在第3个整数之后,我们把它记作3-1=2,即认为是在“第2位”。这是因为如果我们把-101.11写成科学计数法的形式,就是-1.0111 × 2^2。我们把指数2作为“小数点位置”的值。
IEEE 754标准规定,对于指数部分,我们需要加上一个偏移量(bias),对于float类型,偏移量是127。因此,实际存储的指数值是2 + 127 = 129,它的二进制表示是10000001。
偏移量的存在,是为了让指数部分能表示负数(即小数点向右移动的情况),但又不需要专门的符号位。例如0.001101表示为1.101 × 2^-3,指数是-3,加上偏移量127后,存储的值是124,二进制表示为01111100。 - 尾数部分:我们只需要存储有效数字部分
1.0111,由于一个二进制数的最高位一定是1(因为如果是0我们会把它省略,就不是最高位了),因此我们可以去掉前面的1.,它一定是1,不用存储。剩下的0111。由于尾数部分有23位,我们在后面补足0,得到01110000000000000000000。
因此,-5.75在内存中的存储形式是:
1 10000001 01110000000000000000000对于double和long double,它们的存储方式类似,但分配的位数不同,能表示的数值范围和精度也不同。例如double类型占用8个字节(64位),包含1位符号位、11位指数部分和52位尾数部分。
float能表示的数据范围大约是±1.2E-38到±3.4E+38,而double能表示的数据范围大约是±2.3E-308到±1.7E+308。
我们需要唯一记住的是:float类型能表示的数值精度大约是7位十进制数;而double类型能表示的数值精度大约是15-16位十进制数。
五、内存与寻址
我们已经知道,内存是一片偌大的存储空间,里面有很多“位”来存储一个1或0。而这些“位”是被组织成“字节”来存储数据的。每一个变量都占有一些字节,或是1字节,或是4字节,或是8字节等等。那么,这些字节在内存中都在什么样的位置?
计算机通过地址(Address)来标识内存中的每一个字节。每一个字节都有一个唯一的地址,就像我们家里的每一个房间都有一个门牌号一样。
例如,我们可以假设内存的地址从0开始,依次递增。第一个字节的地址是0,第二个字节的地址是1,以此类推。
在现代计算机系统中,地址通常是以十六进制表示的,因为十六进制更紧凑,更容易阅读。十六进制以0x作为标识符开头,例如0x1A3F,代表的是1A3F这个十六进制数,换成十进制是第6719号字节。
内存的一个重要性质,是对于某一变量,它的地址是连续分配的。
例如以某一int类型变量为例,int类型大小是4字节,因此它将占用某四个字节的空间。这四个字节一定是连续的,例如地址1、2、3、4。而不会是例如地址1、3、5、7这样分散储存的。
而另外一个需要注意的点,是两个变量不一定是连续储存的。因此,两个变量可能相隔很远,也可能很近。
来看一个具体例子:
int number = 100;
char letter = 'A';- 假设
number储存在地址1000,number占用4字节,那么地址1000、1001、1002、1003这4个字节都属于number。 letter占用1字节,但即使他在源码中的声明和number紧挨着,它也不一定会被分配在地址1004。它可能被分配在地址1008,或者2000等等更远的地址,这取决于编译器的内存分配策略。- 这些地址和分配过程是由编译器自动完成的,我们只需关注变量和它们的类型。
七、为何要理解内存与数据类型?
- 高效编程:合理选择数据类型可以节省内存空间,提高程序运行效率。
- 防止错误:错误的数据类型选择可能导致数据丢失或程序异常运行。
- 为后续知识打基础:理解内存和数据类型是学习数组、结构体、指针等高级内容的必要前提。
八、易混淆点与补充说明
1. 为什么不是所有变量都占用同样空间?
因为不同类型的数据需要表达的信息量不同。例如,char只需要存储一个字符,而double要存储一个精确到小数点后多位的大数字。
2. 数据如何在内存中排列?
虽然我们声明变量时是顺序写的,但内存中的实际摆放可能会因为对齐(alignment)和优化而发生调整。初学阶段只需理解每个变量都有自己的空间即可。
3. 内存地址到底长什么样?
内存地址通常是一个数字,比如 1024、2048 等。它们是计算机用来定位数据的“导航标志”。
九、练习
1. 声明三个变量,一个整数、一个字符、一个浮点数。并说明每个变量在内存中占用多少字节。
2. 假设有如下变量声明:
int x = 5;
char y = 'B';
float z = 3.14;请问它们分别在内存中占用多少字节?它们的地址可能是什么样的?
3. 用自己的话简述:为什么不同类型的数据在内存中占用的空间不同?
本节内容为后续深入学习数组、结构体、指针等更复杂的数据存储方式奠定了基础。内存和数据类型的关系,是理解程序运行机制的关键环节。





Comments | NOTHING